The Power of Compounding

Compounding refers to the rate at which money grows if you automatically reinvest all the profit you make in the same investment.

To help you understand the concept of compounding, we will use a simple example of a bank account that pays interest. A bank can pay you two kinds of interest: simple interest or compound interest.

Simple Interest Calculation

Suppose you have $1,000 in the bank that pays 10% simple interest per year for 10 years.  Each year, you will earn $100 interest on your $1,000 investment (in the bank account) as calculated below:

Yearly Interest = Yearly Interest Percentage x Deposit Amount
Yearly Interest  = 10% x $1,000  = .1 x $1,000 = $100

The yearly simple interest for the 10-year period is shown below:

As you can see, the total amount of simple interest earned in the 10-year period is $1,000. We calculated this amount by multiplying the yearly interest of 10% by the initial amount you deposited in your account (the principal balance of $1,000) and adding up the resulting products for the 10-year period. Since you get back your initial principal balance of $1,000, you will receive a total of $2,000 at the end of the 10-year period. Remember that this simple interest method shown in the example above assumes that your yearly profit of $100 is not reinvested into the account.

Compound Interest Calculation

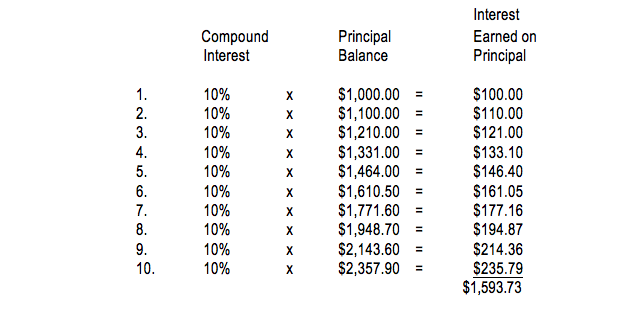
If the bank tells you that you will earn 10% yearly compound interest on your deposit (instead of 10% simple interest), you will make more on your investment than in the simple interest case. Once again, on a yearly basis, you will be earning 10% profit on your principal. But the difference in this case is that your yearly profit (i.e. your yearly interest) will be reinvested each year into the bank account, and not taken out, as was the case with the simple interest calculation above. Here is how your money will stack up each year with compound interest:

With yearly compounding, the interest earned in one year is reinvested into the bank account in the next year. You can tell that this is the case because the Principal Balance column above is increasing, so interest is applied to a bigger and bigger principal balance each year. With the yearly compound interest method, the principal balance increases from $1,000 in the first year to $2,357.90 in the tenth year. With the simple interest method, the principal balance stays at $1,000 for all ten years. At the end of the tenth year for the yearly compound interest example, the total interest earned is $1,593.73 as opposed to $1,000 with simple interest—a difference of $593.73.

Compounding can be done yearly (as is the case in our example), monthly, daily, or in any other time interval.

The True Significance of Compounding

In our prior two examples, the total compound interest was higher than the total simple interest by $593.73. This may seem like a small number, but remember that we assumed you deposited only $1,000 for a 10-year period. As the initial deposit balance increases, the difference between compounding interest and simple interest gets bigger and bigger. And the longer the money stays in the account (or in the investment), the bigger the difference.

The reason we are telling you all of this is because compounding also has a big effect on the money you put into stocks, bonds, mutual funds, and other investments. We will now apply this concept to the return on investment in stocks.

Recall from our introduction that over the past 90 years, the average return on investment for stocks was around  11% per year. This means that on the average, someone investing in stocks (and reinvesting all her dividends as well) could have made 11% profit each year over a long, long time. Because of the compounding effect of investments, a long-term investor can double her money every seven or eight years if we assume an 11% annual profit. Imagine the profit if the investment balance were bigger. This multiplication effect of invested money is one of the reasons it is wise to invest for the long run. 

Compounding and the Rule of 72

The power of compounding is so important to investors that a formula called the rule of 72 has been devised to tell any investor about how much time it will take to double her money, given a yearly compound rate. The rule of 72 states that if you divide 72 by an assumed compound rate, you would get the approximate number of years it will take to double your money. The formula is as follows:

Time to Double Your Money = 72 / Interest Rate

So, if the compound rate is 11%, the formula is as follows:

Time to Double Your Money = 72 / 11 = 6.55 years

Thus, the approximate time to double your money at a compound rate of 11% per year is 6.55 years (or about 7 years). At a compound rate of 22% per year, it will take about 3.27 years (72 / 22 = 3.27 years).